LaTeX Equation to PNG Converter
LaTeX Formula Template Reference
Algebra
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $\left(x-1\right)\left(x+3\right)$ | \left(x-1\right)\left(x+3\right) | $\sqrt{a^2+b^2}$ | \sqrt{a^2+b^2} |
| $\left ( \frac{a}{b}\right )^{n}= \frac{a^{n}}{b^{n}} $ | \left ( \frac{a}{b}\right )^{n}= \frac{a^{n}}{b^{n}} | $\frac{a}{b}\pm \frac{c}{d}= \frac{ad \pm bc}{bd} $ | \frac{a}{b}\pm \frac{c}{d}= \frac{ad \pm bc}{bd} |
| $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 $ | \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 | $\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a},a\ge 0\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a},a\ge 0 $ | \frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a},a\ge 0\frac{1}{\sqrt{a}}=\frac{\sqrt{a}}{a},a\ge 0 |
| $\sqrt[n]{a^{n}}=\left ( \sqrt[n]{a}\right )^{n} $ | \sqrt[n]{a^{n}}=\left ( \sqrt[n]{a}\right )^{n} | $x ={-b \pm \sqrt{b^2-4ac}\over 2a} $ | x ={-b \pm \sqrt{b^2-4ac}\over 2a} |
| $y-y_{1}=k \left( x-x_{1}\right) $ | y-y_{1}=k \left( x-x_{1}\right) | $\left\{\begin{matrix} x=a + r\text{cos}\theta \\ y=b + r\text{sin}\theta \end{matrix}\right. $ | \left\{\begin{matrix} x=a + r\text{cos}\theta \\ y=b + r\text{sin}\theta \end{matrix}\right. |
| $\begin{array}{l} \text{对于方程形如:}x^{3}-1=0 \\ \text{设}\text{:}\omega =\frac{-1+\sqrt{3}i}{2} \\ x_{1}=1,x_{2}= \omega =\frac{-1+\sqrt{3}i}{2} \\ x_{3}= \omega ^{2}=\frac{-1-\sqrt{3}i}{2} \end{array} $ | \begin{array}{l} \text{对于方程形如:}x^{3}-1=0 \\ \text{设}\text{:}\omega =\frac{-1+\sqrt{3}i}{2} \\ x_{1}=1,x_{2}= \omega =\frac{-1+\sqrt{3}i}{2} \\ x_{3}= \omega ^{2}=\frac{-1-\sqrt{3}i}{2} \end{array} | $\begin{array}{l} a\mathop{{x}}\nolimits^{{2}}+bx+c=0 \\ \Delta =\mathop{{b}}\nolimits^{{2}}-4ac \\ \left\{\begin{matrix} \Delta \gt 0\text{方程有两个不相等的实根} \\ \Delta = 0\text{方程有两个相等的实根} \\ \Delta \lt 0\text{方程无实根} \end{matrix}\right. \end{array} $ | \begin{array}{l} a\mathop{{x}}\nolimits^{{2}}+bx+c=0 \\ \Delta =\mathop{{b}}\nolimits^{{2}}-4ac \\ \left\{\begin{matrix} \Delta \gt 0\text{方程有两个不相等的实根} \\ \Delta = 0\text{方程有两个相等的实根} \\ \Delta \lt 0\text{方程无实根} \end{matrix}\right. \end{array} |
| $\begin{array}{l} a\mathop{{x}}\nolimits^{{2}}+bx+c=0 \\ \Delta =\mathop{{b}}\nolimits^{{2}}-4ac \\ \mathop{{x}}\nolimits_{{1,2}}=\frac{{-b \pm \sqrt{{\mathop{{b}}\nolimits^{{2}}-4ac}}}}{{2a}} \\ \mathop{{x}}\nolimits_{{1}}+\mathop{{x}}\nolimits_{{2}}=-\frac{{b}}{{a}} \\ \mathop{{x}}\nolimits_{{1}}\mathop{{x}}\nolimits_{{2}}=\frac{{c}}{{a}} \end{array} $ | \begin{array}{l} a\mathop{{x}}\nolimits^{{2}}+bx+c=0 \\ \Delta =\mathop{{b}}\nolimits^{{2}}-4ac \\ \mathop{{x}}\nolimits_{{1,2}}=\frac{{-b \pm \sqrt{{\mathop{{b}}\nolimits^{{2}}-4ac}}}}{{2a}} \\ \mathop{{x}}\nolimits_{{1}}+\mathop{{x}}\nolimits_{{2}}=-\frac{{b}}{{a}} \\ \mathop{{x}}\nolimits_{{1}}\mathop{{x}}\nolimits_{{2}}=\frac{{c}}{{a}} \end{array} | |
Geometry
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $\Delta A B C$ | \Delta A B C | $a \parallel c,b \parallel c \Rightarrow a \parallel b $ | a \parallel c,b \parallel c \Rightarrow a \parallel b |
| $l \perp \beta ,l \subset \alpha \Rightarrow \alpha \perp \beta$ | l \perp \beta ,l \subset \alpha \Rightarrow \alpha \perp \beta | $\left.\begin{matrix} a \perp \alpha \\ b \perp \alpha \end{matrix}\right\}\Rightarrow a \parallel b$ | \left.\begin{matrix} a \perp \alpha \\ b \perp \alpha \end{matrix}\right\}\Rightarrow a \parallel b |
| $P \in \alpha ,P \in \beta , \alpha \cap \beta =l \Rightarrow P \in l $ | P \in \alpha ,P \in \beta , \alpha \cap \beta =l \Rightarrow P \in l | $\alpha \perp \beta , \alpha \cap \beta =l,a \subset \alpha ,a \perp l \Rightarrow a \perp \beta $ | \alpha \perp \beta , \alpha \cap \beta =l,a \subset \alpha ,a \perp l \Rightarrow a \perp \beta |
| $\left.\begin{matrix} a \subset \beta ,b \subset \beta ,a \cap b=P \\ a \parallel \partial ,b \parallel \partial \end{matrix}\right\}\Rightarrow \beta \parallel \alpha $ | \left.\begin{matrix} a \subset \beta ,b \subset \beta ,a \cap b=P \\ a \parallel \partial ,b \parallel \partial \end{matrix}\right\}\Rightarrow \beta \parallel \alpha | $\alpha \parallel \beta , \gamma \cap \alpha =a, \gamma \cap \beta =b \Rightarrow a \parallel b $ | \alpha \parallel \beta , \gamma \cap \alpha =a, \gamma \cap \beta =b \Rightarrow a \parallel b |
| $A \in l,B \in l,A \in \alpha ,B \in \alpha \Rightarrow l \subset \alpha $ | A \in l,B \in l,A \in \alpha ,B \in \alpha \Rightarrow l \subset \alpha | $\left.\begin{matrix} m \subset \alpha ,n \subset \alpha ,m \cap n=P \\ a \perp m,a \perp n \end{matrix}\right\}\Rightarrow a \perp \alpha $ | \left.\begin{matrix} m \subset \alpha ,n \subset \alpha ,m \cap n=P \\ a \perp m,a \perp n \end{matrix}\right\}\Rightarrow a \perp \alpha |
| $\begin{array}{c} \text{直角三角形中,直角边长a,b,斜边边长c} \\ a^{2}+b^{2}=c^{2} \end{array}$ | \begin{array}{c} \text{直角三角形中,直角边长a,b,斜边边长c} \\ a^{2}+b^{2}=c^{2} \end{array} | |
Inequality
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $a > b,b > c \Rightarrow a > c $ | a > b,b > c \Rightarrow a > c | $a > b,c > d \Rightarrow a+c > b+d $ | a > b,c > d \Rightarrow a+c > b+d |
| $a > b > 0,c > d > 0 \Rightarrow ac bd $ | a > b > 0,c > d > 0 \Rightarrow ac bd | $\begin{array}{c} a \gt b,c \gt 0 \Rightarrow ac \gt bc \\ a \gt b,c \lt 0 \Rightarrow ac \lt bc \end{array}$ | \begin{array}{c} a \gt b,c \gt 0 \Rightarrow ac \gt bc \\ a \gt b,c \lt 0 \Rightarrow ac \lt bc \end{array} |
| $\left | a-b \right | \geqslant \left | a \right | -\left | b \right | $ | \left | a-b \right | \geqslant \left | a \right | -\left | b \right | | $-\left | a \right |\leq a\leqslant \left | a \right |$ | -\left | a \right |\leq a\leqslant \left | a \right | |
| $\left | a \right |\leqslant b \Rightarrow -b \leqslant a \leqslant \left | b \right | $ | \left | a \right |\leqslant b \Rightarrow -b \leqslant a \leqslant \left | b \right | | $\left | a+b \right | \leqslant \left | a \right | + \left | b \right | $ | \left | a+b \right | \leqslant \left | a \right | + \left | b \right | |
| $\begin{array}{c} a \gt b \gt 0,n \in N^{\ast},n \gt 1 \\ \Rightarrow a^{n}\gt b^{n}, \sqrt[n]{a}\gt \sqrt[n]{b} \end{array}$ | \begin{array}{c} a \gt b \gt 0,n \in N^{\ast},n \gt 1 \\ \Rightarrow a^{n}\gt b^{n}, \sqrt[n]{a}\gt \sqrt[n]{b} \end{array} | $\left( \sum_{k=1}^n a_k b_k \right)^{\!\!2}\leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) $ | \left( \sum_{k=1}^n a_k b_k \right)^{\!\!2}\leq \left( \sum_{k=1}^n a_k^2 \right) \left( \sum_{k=1}^n b_k^2 \right) |
| $\begin{array}{c} a,b \in R^{+} \\ \Rightarrow \frac{a+b}{{2}}\ge \sqrt{ab} \\ \left( \text{当且仅当}a=b\text{时取“}=\text{”号}\right) \end{array}$ | \begin{array}{c} a,b \in R^{+} \\ \Rightarrow \frac{a+b}{{2}}\ge \sqrt{ab} \\ \left( \text{当且仅当}a=b\text{时取“}=\text{”号}\right) \end{array} | $\begin{array}{c} a,b \in R \\ \Rightarrow a^{2}+b^{2}\gt 2ab \\ \left( \text{当且仅当}a=b\text{时取“}=\text{”号}\right)\end{array}$ | \begin{array}{c} a,b \in R \\ \Rightarrow a^{2}+b^{2}\gt 2ab \\ \left( \text{当且仅当}a=b\text{时取“}=\text{”号}\right)\end{array} |
| $\begin{array}{c} H_{n}=\frac{n}{\sum \limits_{i=1}^{n}\frac{1}{x_{i}}}= \frac{n}{\frac{1}{x_{1}}+ \frac{1}{x_{2}}+ \cdots + \frac{1}{x_{n}}} \\ G_{n}=\sqrt[n]{\prod \limits_{i=1}^{n}x_{i}}= \sqrt[n]{x_{1}x_{2}\cdots x_{n}} \\ A_{n}=\frac{1}{n}\sum \limits_{i=1}^{n}x_{i}=\frac{x_{1}+ x_{2}+ \cdots + x_{n}}{n} \\ Q_{n}=\sqrt{\sum \limits_{i=1}^{n}x_{i}^{2}}= \sqrt{\frac{x_{1}^{2}+ x_{2}^{2}+ \cdots + x_{n}^{2}}{n}} \\ H_{n}\leq G_{n}\leq A_{n}\leq Q_{n} \end{array}$ | \begin{array}{c} H_{n}=\frac{n}{\sum \limits_{i=1}^{n}\frac{1}{x_{i}}}= \frac{n}{\frac{1}{x_{1}}+ \frac{1}{x_{2}}+ \cdots + \frac{1}{x_{n}}} \\ G_{n}=\sqrt[n]{\prod \limits_{i=1}^{n}x_{i}}= \sqrt[n]{x_{1}x_{2}\cdots x_{n}} \\ A_{n}=\frac{1}{n}\sum \limits_{i=1}^{n}x_{i}=\frac{x_{1}+ x_{2}+ \cdots + x_{n}}{n} \\ Q_{n}=\sqrt{\sum \limits_{i=1}^{n}x_{i}^{2}}= \sqrt{\frac{x_{1}^{2}+ x_{2}^{2}+ \cdots + x_{n}^{2}}{n}} \\ H_{n}\leq G_{n}\leq A_{n}\leq Q_{n} \end{array} |
Integral
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $\frac{\mathrm{d}}{\mathrm{d}x}x^n=nx^{n-1} $ | \frac{\mathrm{d}}{\mathrm{d}x}x^n=nx^{n-1} | $\frac{\mathrm{d}}{\mathrm{d}x}e^{ax}=a\,e^{ax} $ | \frac{\mathrm{d}}{\mathrm{d}x}e^{ax}=a\,e^{ax} |
| $\frac{\mathrm{d}}{\mathrm{d}x}\ln(x)=\frac{1}{x} $ | \frac{\mathrm{d}}{\mathrm{d}x}\ln(x)=\frac{1}{x} | $\frac{\mathrm{d}}{\mathrm{d}x}\sin x=\cos x $ | \frac{\mathrm{d}}{\mathrm{d}x}\sin x=\cos x |
| $\frac{\mathrm{d}}{\mathrm{d}x}\cos x=-\sin x $ | \frac{\mathrm{d}}{\mathrm{d}x}\cos x=-\sin x | $\int k\mathrm{d}x = kx+C $ | \int k\mathrm{d}x = kx+C |
| $\frac{\mathrm{d}}{\mathrm{d}x}\tan x=\sec^2 x $ | \frac{\mathrm{d}}{\mathrm{d}x}\tan x=\sec^2 x | $\frac{\mathrm{d}}{\mathrm{d}x}\cot x=-\csc^2 x $ | \frac{\mathrm{d}}{\mathrm{d}x}\cot x=-\csc^2 x |
| $\int \frac{1}{x}\mathrm{d}x= \ln \left| x \right| +C $ | \int \frac{1}{x}\mathrm{d}x= \ln \left| x \right| +C | $\int \frac{1}{\sqrt{1-x^{2}}}\mathrm{d}x= \arcsin x +C $ | \int \frac{1}{\sqrt{1-x^{2}}}\mathrm{d}x= \arcsin x +C |
| $\int \frac{1}{1+x^{2}}\mathrm{d}x= \arctan x +C $ | \int \frac{1}{1+x^{2}}\mathrm{d}x= \arctan x +C | $\int u \frac{\mathrm{d}v}{\mathrm{d}x}\,\mathrm{d}x=uv-\int \frac{\mathrm{d}u}{\mathrm{d}x}v\,\mathrm{d}x $ | \int u \frac{\mathrm{d}v}{\mathrm{d}x}\,\mathrm{d}x=uv-\int \frac{\mathrm{d}u}{\mathrm{d}x}v\,\mathrm{d}x |
| $f(x) = \int_{-\infty}^\infty \hat f(x)\xi\,e^{2 \pi i \xi x} \,\mathrm{d}\xi $ | f(x) = \int_{-\infty}^\infty \hat f(x)\xi\,e^{2 \pi i \xi x} \,\mathrm{d}\xi | $\int x^{\mu}\mathrm{d}x=\frac{x^{\mu +1}}{\mu +1}+C, \left({\mu \neq -1}\right) $ | \int x^{\mu}\mathrm{d}x=\frac{x^{\mu +1}}{\mu +1}+C, \left({\mu \neq -1}\right) |
Matrix
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} $ | \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} | $\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} $ | \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} |
| $\begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{pmatrix} $ | \begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \ddots & \vdots \\ a_{m1} & \cdots & a_{mn} \end{pmatrix} | $\begin{array}{c} A=A^{T} \\ A=-A^{T} \end{array}$ | \begin{array}{c} A=A^{T} \\ A=-A^{T} \end{array} |
| $O = \begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix} $ | O = \begin{bmatrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix} | $A_{m\times n}= \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}& a_{m2}& \cdots & a_{mn} \end{bmatrix} =\left [ a_{ij}\right ] $ | A_{m\times n}= \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}& a_{m2}& \cdots & a_{mn} \end{bmatrix} =\left [ a_{ij}\right ] |
| $\begin{array}{c} A={\left[ a_{ij}\right]_{m \times n}},B={\left[ b_{ij}\right]_{n \times s}} \\ c_{ij}= \sum \limits_{k=1}^{{n}}a_{ik}b_{kj} \\ C=AB=\left[ c_{ij}\right]_{m \times s} = \left[ \sum \limits_{k=1}^{n}a_{ik}b_{kj}\right]_{m \times s} \end{array}$ | \begin{array}{c} A={\left[ a_{ij}\right]_{m \times n}},B={\left[ b_{ij}\right]_{n \times s}} \\ c_{ij}= \sum \limits_{k=1}^{{n}}a_{ik}b_{kj} \\ C=AB=\left[ c_{ij}\right]_{m \times s} = \left[ \sum \limits_{k=1}^{n}a_{ik}b_{kj}\right]_{m \times s} \end{array} | $\mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i}& \mathbf{j}& \mathbf{k} \\ \frac{\partial X}{\partial u}& \frac{\partial Y}{\partial u}& 0 \\ \frac{\partial X}{\partial v}& \frac{\partial Y}{\partial v}& 0 \\ \end{vmatrix} $ | \mathbf{V}_1 \times \mathbf{V}_2 = \begin{vmatrix} \mathbf{i}& \mathbf{j}& \mathbf{k} \\ \frac{\partial X}{\partial u}& \frac{\partial Y}{\partial u}& 0 \\ \frac{\partial X}{\partial v}& \frac{\partial Y}{\partial v}& 0 \\ \end{vmatrix} |
Trigonometric Functions
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $e^{i \theta} $ | e^{i \theta} | $\left(\frac{\pi}{2}-\theta \right ) $ | \left(\frac{\pi}{2}-\theta \right ) |
| $\text{sin}^{2}\frac{\alpha}{2}=\frac{1- \text{cos}\alpha}{2} $ | \text{sin}^{2}\frac{\alpha}{2}=\frac{1- \text{cos}\alpha}{2} | $\text{cos}^{2}\frac{\alpha}{2}=\frac{1+ \text{cos}\alpha}{2} $ | \text{cos}^{2}\frac{\alpha}{2}=\frac{1+ \text{cos}\alpha}{2} |
| $\text{tan}\frac{\alpha}{2}=\frac{\text{sin}\alpha}{1+ \text{cos}\alpha} $ | \text{tan}\frac{\alpha}{2}=\frac{\text{sin}\alpha}{1+ \text{cos}\alpha} | $\sin \alpha + \sin \beta =2 \sin \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} $ | \sin \alpha + \sin \beta =2 \sin \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} |
| $\sin \alpha - \sin \beta =2 \cos \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} $ | \sin \alpha - \sin \beta =2 \cos \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} | $\cos \alpha + \cos \beta =2 \cos \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} $ | \cos \alpha + \cos \beta =2 \cos \frac{\alpha + \beta}{2}\cos \frac{\alpha - \beta}{2} |
| $\cos \alpha - \cos \beta =-2\sin \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} $ | \cos \alpha - \cos \beta =-2\sin \frac{\alpha + \beta}{2}\sin \frac{\alpha - \beta}{2} | $a^{2}=b^{2}+c^{2}-2bc\cos A $ | a^{2}=b^{2}+c^{2}-2bc\cos A |
| $\frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}=\frac{1}{2R} $ | \frac{\sin A}{a}=\frac{\sin B}{b}=\frac{\sin C}{c}=\frac{1}{2R} | $\sin \left ( \frac{\pi}{2}-\alpha \right ) = \cos \alpha $ | \sin \left ( \frac{\pi}{2}-\alpha \right ) = \cos \alpha |
| $\sin \left ( \frac{\pi}{2}+\alpha \right ) = \cos \alpha $ | \sin \left ( \frac{\pi}{2}+\alpha \right ) = \cos \alpha | |
Statistics
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $C_{r}^{n} $ | C_{r}^{n} | $\frac{n!}{r!(n-r)!} $ | \frac{n!}{r!(n-r)!} |
| $\sum_{i=1}^{n}{X_i} $ | \sum_{i=1}^{n}{X_i} | $\sum_{i=1}^{n}{X_i^2} $ | \sum_{i=1}^{n}{X_i^2} |
| $X_1, \cdots,X_n $ | X_1, \cdots,X_n | $\frac{x-\mu}{\sigma} $ | \frac{x-\mu}{\sigma} |
| $\sum_{i=1}^{n}{(X_i - \overline{X})^2} $ | \sum_{i=1}^{n}{(X_i - \overline{X})^2} | $\begin{array}{c} \text{若}P \left( AB \right) =P \left( A \right) P \left( B \right) \\ \text{则}P \left( A \left| B\right. \right) =P \left({B}\right) \end{array}$ | \begin{array}{c} \text{若}P \left( AB \right) =P \left( A \right) P \left( B \right) \\ \text{则}P \left( A \left| B\right. \right) =P \left({B}\right) \end{array} |
| $P(E) ={n \choose k}p^k (1-p)^{n-k} $ | P(E) ={n \choose k}p^k (1-p)^{n-k} | $P \left( A \right) = \lim \limits_{n \to \infty}f_{n}\left ( A \right ) $ | P \left( A \right) = \lim \limits_{n \to \infty}f_{n}\left ( A \right ) |
| $P \left( \bigcup \limits_{i=1}^{+ \infty}A_{i}\right) = \prod \limits_{i=1}^{+ \infty}P{\left( A_{i}\right)} $ | P \left( \bigcup \limits_{i=1}^{+ \infty}A_{i}\right) = \prod \limits_{i=1}^{+ \infty}P{\left( A_{i}\right)} | $\begin{array}{c} P \left( \emptyset \right) =0 \\ P \left( S \right) =1 \end{array}$ | \begin{array}{c} P \left( \emptyset \right) =0 \\ P \left( S \right) =1 \end{array} |
| $\begin{array}{c} \forall A \in S \\ P \left( A \right) \ge 0 \end{array}$ | \begin{array}{c} \forall A \in S \\ P \left( A \right) \ge 0 \end{array} | $P \left( \bigcup \limits_{i=1}^{n}A_{i}\right) = \prod \limits_{i=1}^{n}P \left( A_{i}\right) $ | P \left( \bigcup \limits_{i=1}^{n}A_{i}\right) = \prod \limits_{i=1}^{n}P \left( A_{i}\right) |
| $\begin{array}{c} S= \binom{N}{n},A_{k}=\binom{M}{k}\cdot \binom{N-M}{n-k} \\ P\left ( A_{k}\right ) = \frac{\binom{M}{k}\cdot \binom{N-M}{n-k}}{\binom{N}{n}} \end{array}$ | \begin{array}{c} S= \binom{N}{n},A_{k}=\binom{M}{k}\cdot \binom{N-M}{n-k} \\ P\left ( A_{k}\right ) = \frac{\binom{M}{k}\cdot \binom{N-M}{n-k}}{\binom{N}{n}} \end{array} | $\begin{array}{c} P_{n}=n! \\ A_{n}^{k}=\frac{n!}{\left( n-k \left) !\right. \right.} \end{array}$ | \begin{array}{c} P_{n}=n! \\ A_{n}^{k}=\frac{n!}{\left( n-k \left) !\right. \right.} \end{array} |
Sequence
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $a_{n}=a_{1}q^{n-1} $ | a_{n}=a_{1}q^{n-1} | $a_{n}=a_{1}+ \left( n-1 \left) d\right. \right. $ | a_{n}=a_{1}+ \left( n-1 \left) d\right. \right. |
| $S_{n}=na_{1}+\frac{n \left( n-1 \right)}{{2}}d$ | S_{n}=na_{1}+\frac{n \left( n-1 \right)}{{2}}d | $S_{n}=\frac{n \left( a_{1}+a_{n}\right)}{2} $ | S_{n}=\frac{n \left( a_{1}+a_{n}\right)}{2} |
| $\frac{1}{n \left( n+k \right)}= \frac{1}{k}\left( \frac{1}{n}-\frac{1}{n+k}\right) $ | \frac{1}{n \left( n+k \right)}= \frac{1}{k}\left( \frac{1}{n}-\frac{1}{n+k}\right) | $\frac{1}{n^{2}-1}= \frac{1}{2}\left( \frac{1}{n-1}-\frac{1}{n+1}\right) $ | \frac{1}{n^{2}-1}= \frac{1}{2}\left( \frac{1}{n-1}-\frac{1}{n+1}\right) |
| $\frac{1}{4n^{2}-1}=\frac{1}{2}\left( \frac{1}{2n-1}-\frac{1}{2n+1}\right) $ | \frac{1}{4n^{2}-1}=\frac{1}{2}\left( \frac{1}{2n-1}-\frac{1}{2n+1}\right) | $\frac{n+1}{n \left( n-1 \left) \cdot 2^{n}\right. \right.}= \frac{1}{\left( n-1 \left) \cdot 2^{n-1}\right. \right.}-\frac{1}{n \cdot 2^{n}} $ | \frac{n+1}{n \left( n-1 \left) \cdot 2^{n}\right. \right.}= \frac{1}{\left( n-1 \left) \cdot 2^{n-1}\right. \right.}-\frac{1}{n \cdot 2^{n}} |
| $\begin{array}{c} \text{若}\left \{a_{n}\right \}、\left \{b_{n}\right \}\text{为等差数列}, \\ \text{则}\left \{a_{n}+ b_{n}\right \}\text{为等差数列} \end{array}$ | \begin{array}{c} \text{若}\left \{a_{n}\right \}、\left \{b_{n}\right \}\text{为等差数列}, \\ \text{则}\left \{a_{n}+ b_{n}\right \}\text{为等差数列} \end{array} | $(1+x)^{n} =1 + \frac{nx}{1!} + \frac{n(n-1)x^{2}}{2!} + \cdots $ | (1+x)^{n} =1 + \frac{nx}{1!} + \frac{n(n-1)x^{2}}{2!} + \cdots |
Physical
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
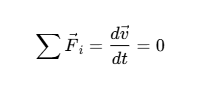 | \sum {{{ \vec{F} }_i}} = \frac{{d \vec{v}}}{{dt}} = 0 | 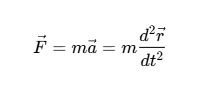 | \vec{F} = m \vec{a} = m \frac{{{d^2} \vec{r} }}{{d{t^2}}} |
 | {{ \vec{F} }_{12}} = - {{ \vec{F} }_{21}} | ${E_p} = -\frac{{GMm}}{r} $ | {E_p} = -\frac{{GMm}}{r} |
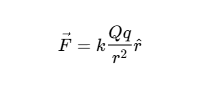 | \vec{F} = k \frac{{Qq}}{{{r^2}}} \hat{r} | 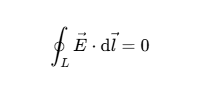 | \oint_L { \vec{E} } \cdot { \rm{d}} \vec{l} = 0 |
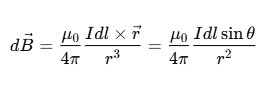 | d \vec{B} = \frac{{{ \mu _0}}}{{4 \pi }} \frac{{Idl \times \vec{r} }}{{{r^3}}} = \frac{{{ \mu _0}}}{{4 \pi }} \frac{{Idl \sin \theta }}{{{r^2}}} | $d \vec{F}= Id \vec{l} \times \vec{B} $ | d \vec{F}= Id \vec{l} \times \vec{B} |
| $E = n{{ \Delta \Phi } \over {\Delta {t} }} $ | E = n{{ \Delta \Phi } \over {\Delta {t} }} | 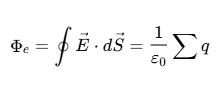 | \mathop \Phi \nolimits_e = \oint { \vec{E} \cdot {d \vec{S}} = {1 \over {{\varepsilon _0}}}\sum {q} } |
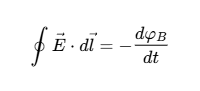 | \oint { \vec{E} \cdot {d\vec{l}} = - {{d{\varphi _B}} \over {dt}}} | 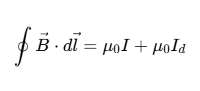 | \oint { \vec{B} \cdot {d \vec{l}} = { \mu _0}} I + { \mu _0}{I_d} |
| $Q = I ^ { 2 } R \mathrm { t } $ | Q = I ^ { 2 } R \mathrm { t } | $F = G{{Mm} \over {{r^2}}} $ | F = G{{Mm} \over {{r^2}}} |
| ${E_k} = hv - {W_0} $ | {E_k} = hv - {W_0} | $\lambda = \frac{{ \frac{{{c^2}}}{v}}}{{ \frac{{m{c^2}}}{h}}} = \frac{h}{{mv}} = \frac{h}{p} $ | \lambda = \frac{{ \frac{{{c^2}}}{v}}}{{ \frac{{m{c^2}}}{h}}} = \frac{h}{{mv}} = \frac{h}{p} |
| $\Delta {x} \Delta {p} \ge \frac{h}{{4 \pi }} $ | \Delta {x} \Delta {p} \ge \frac{h}{{4 \pi }} | $l = {l_0} \sqrt {1 - {{( \frac{v}{c})}^2}} $ | l = {l_0} \sqrt {1 - {{( \frac{v}{c})}^2}} |
| ${y_0} = A \cos ( \omega {t} + { \varphi _0}) $ | {y_0} = A \cos ( \omega {t} + { \varphi _0}) | $y(t) = A \cos ( \frac{{2 \pi {x}}}{ \lambda } + \varphi )$ | y(t) = A \cos ( \frac{{2 \pi {x}}}{ \lambda } + \varphi ) |
| $\begin{array}{l} \nabla \cdot \mathbf{E} =\cfrac{\rho}{\varepsilon _0} \\ \nabla \cdot \mathbf{B} = 0 \\ \nabla \times \mathbf{E} = -\cfrac{\partial \mathbf{B}}{\partial t } \\ \nabla \times \mathbf{B} = \mu _0\mathbf{J} + \mu _0\varepsilon_0 \cfrac{\partial \mathbf{E}}{\partial t } \end{array} $ | \begin{array}{l} \nabla \cdot \mathbf{E} =\cfrac{\rho}{\varepsilon _0} \\ \nabla \cdot \mathbf{B} = 0 \\ \nabla \times \mathbf{E} = -\cfrac{\partial \mathbf{B}}{\partial t } \\ \nabla \times \mathbf{B} = \mu _0\mathbf{J} + \mu _0\varepsilon_0 \cfrac{\partial \mathbf{E}}{\partial t } \end{array} | $\begin{array}{l} {\huge \oiint}_\mathbb{S} \mathbf{E} \cdot\mathrm{d}s= \cfrac{Q}{\varepsilon_0} \\ {\huge \oiint}_\mathbb{S} \mathbf{B} \cdot\mathrm{d}s= 0 \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{E} \cdot \mathrm{d}l=-\cfrac{\mathrm{d}\Phi _{\mathbf{B}}}{\mathrm{d}t } \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{B} \cdot \mathrm{d}l=\mu_0I+ \mu_0 \varepsilon_0\cfrac{\mathrm{d}\Phi _{\mathbf{E}}}{\mathrm{d}t } \end{array} $ | \begin{array}{l} {\huge \oiint}_\mathbb{S} \mathbf{E} \cdot\mathrm{d}s= \cfrac{Q}{\varepsilon_0} \\ {\huge \oiint}_\mathbb{S} \mathbf{B} \cdot\mathrm{d}s= 0 \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{E} \cdot \mathrm{d}l=-\cfrac{\mathrm{d}\Phi _{\mathbf{B}}}{\mathrm{d}t } \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{B} \cdot \mathrm{d}l=\mu_0I+ \mu_0 \varepsilon_0\cfrac{\mathrm{d}\Phi _{\mathbf{E}}}{\mathrm{d}t } \end{array} |
| $\begin{array}{l} \nabla \cdot \mathbf{D} =\rho _f \\ \nabla \cdot \mathbf{B} = 0 \\ \nabla \times \mathbf{E} = -\cfrac{\partial \mathbf{B}}{\partial t } \\ \nabla \times \mathbf{H} = \mathbf{J}_f + \cfrac{\partial \mathbf{D}}{\partial t } \end{array} $ | \begin{array}{l} \nabla \cdot \mathbf{D} =\rho _f \\ \nabla \cdot \mathbf{B} = 0 \\ \nabla \times \mathbf{E} = -\cfrac{\partial \mathbf{B}}{\partial t } \\ \nabla \times \mathbf{H} = \mathbf{J}_f + \cfrac{\partial \mathbf{D}}{\partial t } \end{array} | $\begin{array}{l} {\huge \oiint}_\mathbb{S} \mathbf{D} \cdot\mathrm{d}s= Q_f \\ {\huge \oiint}_\mathbb{S} \mathbf{B} \cdot\mathrm{d}s= 0 \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{E} \cdot \mathrm{d}l=-\cfrac{\mathrm{d}\Phi _{\mathbf{B}}}{\mathrm{d}t } \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{H} \cdot \mathrm{d}l=I_f+\cfrac{\mathrm{d}\Phi _{\mathbf{D}}}{\mathrm{d}t } \end{array} $ | \begin{array}{l} {\huge \oiint}_\mathbb{S} \mathbf{D} \cdot\mathrm{d}s= Q_f \\ {\huge \oiint}_\mathbb{S} \mathbf{B} \cdot\mathrm{d}s= 0 \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{E} \cdot \mathrm{d}l=-\cfrac{\mathrm{d}\Phi _{\mathbf{B}}}{\mathrm{d}t } \\ {\huge \oint}_{\mathbb{L}}^{} \mathbf{H} \cdot \mathrm{d}l=I_f+\cfrac{\mathrm{d}\Phi _{\mathbf{D}}}{\mathrm{d}t } \end{array}
|
Chemical
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
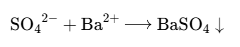 | \ce{SO4^2- + Ba^2+ -> BaSO4 v} | 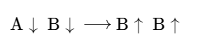 | \ce{A v B (v) -> B ^ B (^)} |
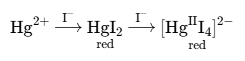 | \ce{Hg^2+ ->[I-] $\underset{\mathrm{red}}{\ce{HgI2}}$ ->[I-] $\underset{\mathrm{red}}{\ce{[Hg^{II}I4]^2-}}$} | 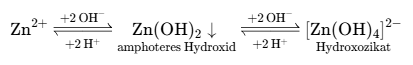 | \ce{Zn^2+ <=>[+ 2OH-][+ 2H+] $\underset{\text{amphoteres Hydroxid}}{\ce{Zn(OH)2 v}}$ <=>[+ 2OH-][+ 2H+] $\underset{\text{Hydroxozikat}}{\ce{[Zn(OH)4]^2-}}$} |
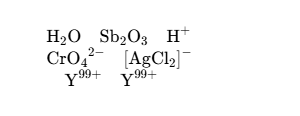 | \ce{H2O}\quad \ce{Sb2O3} \quad\ce{H+} \\\ce{CrO4^2-} \quad\ce{[AgCl2]-} \\\quad\ce{Y^99+} \quad\ce{Y^{99+}} | 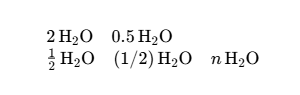 | \ce{2H2O} \quad\ce{0.5 H2O} \\\ce{1/2H2O} \quad\ce{(1/2)H2O} \quad\ce{$n$ H2O} |
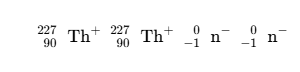 | \ce{^{227}_{90}Th+} \quad\ce{^227_90Th+} \quad\ce{^{0}_{-1}n^{-}} \quad\ce{^0_-1n-} | 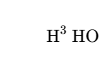 | \ce{H^3 HO} |
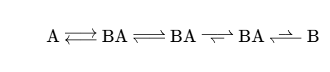 | \ce{A <--> B} \ce{A <=> B} \ce{A <=>> B} \ce{A <<=> B} | 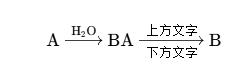 | \ce{A ->[H2O] B} \ce{A ->[{上方文字}][{下方文字}] B} |
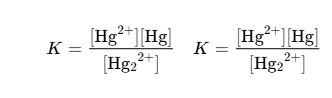 | \ce{$K = \frac{[\ce{Hg^2+}][\ce{Hg}]}{[\ce{Hg2^2+}]}$}\quad\ce{$K = \ce{\frac{[Hg^2+][Hg]}{[Hg2^2+]}}$} | |
Others
| Formulas | LaTeX | Formulas | LaTeX |
|---|---|---|---|
| $x\tfrac{a}{b} $ | x\tfrac{a}{b} | $\mathrm{d}t $ | \mathrm{d}t |
| $\frac{\mathrm{d} y}{\mathrm{d} x} $ | \frac{\mathrm{d} y}{\mathrm{d} x} | $\partial t $ | \partial t |
| $\frac{\partial y}{\partial x} $ | \frac{\partial y}{\partial x} | $\nabla\psi $ | \nabla\psi |
| $ \frac{\partial^2}{\partial x_1\partial x_2}y $ | \frac{\partial^2}{\partial x_1\partial x_2}y | $\cfrac{1}{a + \cfrac{7}{b + \cfrac{2}{9}}} =c $ | \cfrac{1}{a + \cfrac{7}{b + \cfrac{2}{9}}} =c |
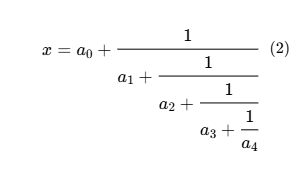 | \begin{equation}x = a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{a_3 + \cfrac{1}{a_4} } } }\end{equation} | ${f}^{(n)} $ | {f}^{(n)} |
| ${f}'' $ | {f}'' | $\sqrt[2]{3} $ | \sqrt[2]{3} |
| $_{a}^{d}x$ | _{a}^{d}x | $x_{a}^{d} $ | x_{a}^{d} |
| $_{a}^{d}x_{a}^{d} $ | _{a}^{d}x_{a}^{d} | $36.5^{\circ} $ | 36.5^{\circ} |
| $\lim_{x \to \infty} $ | \lim_{x \to \infty} | $\lim_{x \to 0} $ | \lim_{x \to 0} |
| $\textstyle \lim_{x \to 0} $ | \textstyle \lim_{x \to 0} | $\max_{x} f$ | \max_{x} f |
| $\log_{2}{5} $ | \log_{2}{5} | $\lg_{2}{4} $ | \lg_{2}{4} |
| $\ln_{2}{10} $ | \ln_{2}{10} | $\sin^{-1} \alpha $ | \sin^{-1} \alpha |
| $\sum_{a}^{b} $ | \sum_{a}^{b} | $ {\textstyle \sum_{a}^{b}} $ | {\textstyle \sum_{a}^{b}} |
| $\prod_{a}^{b} $ | \prod_{a}^{b} | $ {\textstyle \prod_{a}^{b}} $ | {\textstyle \prod_{a}^{b}} |
Create LaTeX Formula online and save the results as PNG images using our intuitive tool. This user-friendly interface allows you to enter LaTeX equations, which are rendered in high-quality graphics, making it easy to include your mathematical expressions in presentations, documents, and online content. Perfect for students, teachers, and professionals in mathematics and science, the LaTeX Equation to PNG tool simplifies the equation rendering process.
- Easy LaTeX Input: Users can easily enter their equations in a designated text area, allowing for one formula per line, which is formatted using standard LaTeX syntax.
- Multiple Output Formats: Choose to render equations as high-quality PNG files or vector-based SVG images, giving users flexibility based on their needs.
- Instant Preview: The tool provides an immediate preview of the rendered equation, making it easy for users to see and adjust their input.
- Flexible Rendering Options: Users can control the display mode, alignment, and minimum width of their equations to fit their desired format.
Write Reply